The Nonequivalent Group Design
In this exercise you are going to create a nonequivalent group
or an untreated control group design of the form
N O X O
N O O
where each O indicates an observation or measure on a group of
people, the X indicates the implementation of some treatment or
program, separate lines are used to depict the two groups in the
study, the N indicates that assignment to either the treatment
or control group is not controlled by the researcher (the groups
may be naturally formed or persons may self-select the group they
are in), and the passage of time is indicated by moving from left
to right. We will assume that we are comparing a program and
comparison group (instead of two programs or different levels
of the same program).
This design has several important characteristics. First, the
design has pretest and posttest measures for all participants.
Second, the design calls for two groups, one which gets some
program or treatment and one which does not (termed the "program"
and "comparison" groups respectively). Third, the
two groups are nonequivalent, that is, we expect that they
may differ prior to the study. Often, nonequivalent groups are
simply two intact groups which are convenient to the researcher
(e.g., two classrooms, two states, two cities, two mental health
centers, etc.).
You will use the pretest and posttest scores from the first exercise
as the basis for this exercise. The first thing you need to do
is to copy the pretest scores from column 5 of Table 1-1 into
column 2 of Table 3-1. Now, you have to divide the 50 participants
into two nonequivalent groups. We can do this in several ways,
but the simplest would be to consider the first 25 persons as
being in the program group and the second 25 as being in the comparison
group. The pretest and posttest scores of these 50 participants
were formed from random rolls of pairs of dice. Be assured, that
on average these two subgroups should have very similar
pretest and posttest means. But in this exercise we want to assume
that the two groups are nonequivalent and so we will have to make
them nonequivalent. The easiest way to make the groups nonequivalent
on the pretest is to add some constant value to all the pretest
scores for persons in one of the groups. To see how you will
do this, look at Table 3-1. You should have already copied the
pretest scores (X) for each participant into column 2. Notice
that column 3 of Table 3-1 has a number "5" in it
for the first 25 participants and a "0" for the second
set of 25 persons. These numbers describe the initial pretest
differences between these groups (i.e., the groups are nonequivalent
on the pretest). To create the pretest scores for this exercise
add the pretest scores from column 2 to the constant values in
column 3 and place the results in column 4 of Table 3-1 under
the heading "Pretest (X) for Nonequivalent Groups".
Note that the choice of a difference of 5 points between the
groups was arbitrary. Also note that in this simulation we have
let the program group have the pretest advantage of 5 points.
Now you need to create posttest scores. You should copy the posttest
scores from column 6 of Table 1-1 directly into column 5 of Table
3-1. In this simulation, we will assume that the program
has an effect and you will add 7 points to the posttest score
of each person in the program group. In Table 3-1, the initial
group difference (i.e., 5 points difference) is listed again in
column 6 and the program effect or gain (i.e., 7 points) in column
7. Therefore, you get the final posttest score by adding the
posttest score from the first exercise (column 5), the group differences
(column 6) and the program effect or gain (column 7). The sum
of these three components should be placed in column 8 of Table
3-1 labeled "Posttest Y for Nonequivalent Groups".
It is useful at this point to stop and consider what you have
done. When you combine the measurement model from the first exercise
with what you have done here, we can represent each personŐs
pretest score with the formula
X = T + D + eX
where
X = the pretest score for a person
T = the true ability or true score (based on the roll of a pair
of dice)
D = initial group difference (D = 5 if the person is in the program
group; D = 0 if in comparison group)
eX = pretest measurement
error (based on the roll of a pair of dice)
Similarly, we can now represent the posttest for each person as
Y = T + D + G + eY
Y = the posttest score for a person
T = the same true ability as for the pretest
D = the same initial group difference as on the pretest
G = the effect of the program or the Gain (G = 7 for persons in
the program; G = 0 for comparison persons)
eY = posttest measurement
error (based on a different roll of the dice than pretest error)
It is important to get a visual impression of the data and so,
as in the first two exercises, you should graph the univariate
and bivariate distributions. Remember that as in the randomized
experimental simulation you need to distinguish the program group
scores from the comparison group scores on all graphs. Graph
the pretest distribution in Figure 3-1, the posttest in Figure
3-2, and the bivariate distribution in Figure 3-3. As before,
you should also estimate the central tendency in the univariate
distributions, taking care to do this separately for each group.
And, you should visually fit a line through the bivariate data,
fitting separate lines for the program and comparison groups.
When all of this is completed you should be convinced of the following:
- There are differences between the program and comparison groups
on the pretest. If you examine the pretest distributions in Figure
3-1, you should see that the central score for the program group
is about 5 points higher than the central score of the comparison
group (this is no surprise because you added in the 5 points).
This difference is typical of what we expect when we use nonequivalent
groups in research and simply tells us that prior to the study
one group is higher than the other on the pretest characteristic.
- There are even larger differences between the groups on the
posttest. In fact, the posttest difference between groups should
be about 12 points (again, this is no surprise because you added
in 5 + 7 points). If this were real data and you were going to
analyze it, you would probably begin to suspect that your program
may have had an effect because the posttest difference exceeds
the pretest difference.
- If you were to graph the central values for the pretest and
posttest for the two groups, you would probably get a picture
that looks something like this:
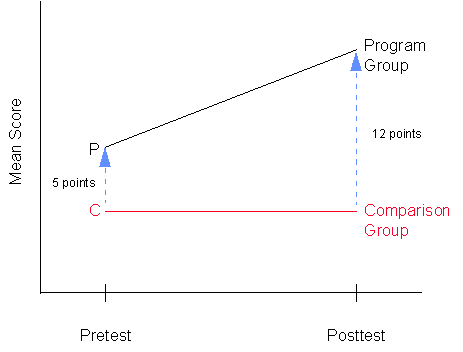
One alternative explanation (for a program effect) that you would
have to consider is the possibility of a selection-maturation
threat, that is, that your two groups are maturing at different
rates. However, you know this is not the case because you specifically
put in the same size group difference of 5 points on both
the pretest and posttest (i.e., in the absence of the program,
the groups did not mature at different rates). Nevertheless,
if you were analyzing data like this in real life, you would have
to assume that in the absence of the program the differences
between the groups were the same on the pretest and posttest and
that any additional difference (in this case 7 points) must be
due to the program. You might know from previous research that
a maturational pattern like the one in the above figure would
be unlikely and rule out the threat as being improbable on that
basis. Nevertheless, it should be apparent that you would be
much better off, if you had a better idea of how the two groups
would have changed from pre to post in the absence of the program.
If you had taken an additional pretest observation (i.e. double
pretest or the "dry run" experiment), you would
have a much better idea of whether selection-maturation is a legitimate
threat. In any event, you should be more firmly convinced of
the importance of selection bias threats in nonequivalent group
designs of this type.
- You should also note what would happen if you analyzed the data
in other ways. Obviously a simple t-test of differences on the
posttest would give an inappropriately large estimate of program
effect -- in this example, it would tell you that the groups differ
by about 12 points, but you know that a good deal of that is due
to initial differences. On the other hand, an analysis of variance
(or t-test) on gain scores would work here but only because
you know that without the program (i.e., if you had not added
the 7 point program effect) the two groups would have gained,
on the average, exactly the same amount (in this simulation, they
would have gained nothing!). You should be convinced then that
the analysis of variance on gain scores relies on the assumption
of equal gain in both groups in the absence of the program.
- You have only simulated one possible outcome of many. You could,
for example, simulate a null case (i.e., no effect of the
program) simply by omitting the 7 points added to the program
group persons. You could have a constant maturation rate
by adding a constant value to all posttest scores. Or, you could
simulate a selection-maturation problem by adding different
constants to the posttest scores (or true scores) of the two groups.
Or you could start out with an inferior program group
by adding the group difference to the comparison group instead.
- Finally, you should also recognize an important fact about selection
bias which is not illustrated in this exercise. When we select
nonequivalent groups we expect that they may differ on one or
more characteristics prior to the study. If we find that the
pretest scores of our two groups are equal, we cannot assume
that there is no selection bias or difference between the groups.
The pretest averages could be equal by chance or the groups could
differ on any number of other characteristics that are not measured
by the pretest but nevertheless affect the posttest scores. We
cannot conduct a t-test on pretest differences, find that there
is no significant difference and conclude that selection bias
is not a problem. Selection bias occurs whenever our groups differ
on some pre-study characteristic that affects the posttest and
when this pre-study difference is not perfectly described
or "accounted for" by the difference on the pretest.
Nonequivalent Group Design
Table 3-1
| 1 | 2
| 3 | 4
| 5 | 6
| 7 | 8
|
| Person | Pretest
X
from
Table 1-1
| Pretest
Group
Difference
| Pretest
(X) for
Nonequi-
valent
Groups
| Posttest
Y
from
Table 1-1
| Posttest
Group
Difference
| Effect of
Program
(G)
| Posttest
(Y) for
Nonequi-valent
Groups
|
| 1 |
|
5 |
|
|
5 |
7 |
|
| 2 |
|
5 |
|
|
5 |
7 |
|
| 3 |
|
5 |
|
|
5 |
7 |
|
| 4 |
|
5 |
|
|
5 |
7 |
|
| 5 |
|
5 |
|
|
5 |
7 |
|
| 6 |
|
5 |
|
|
5 |
7 |
|
| 7 |
|
5 |
|
|
5 |
7 |
|
| 8 |
|
5 |
|
|
5 |
7 |
|
| 9 |
|
5 |
|
|
5 |
7 |
|
| 10 |
|
5 |
|
|
5 |
7 |
|
| 11 |
|
5 |
|
|
5 |
7 |
|
| 12 |
|
5 |
|
|
5 |
7 |
|
| 13 |
|
5 |
|
|
5 |
7 |
|
| 14 |
|
5 |
|
|
5 |
7 |
|
| 15 |
|
5 |
|
|
5 |
7 |
|
| 16 |
|
5 |
|
|
5 |
7 |
|
| 17 |
|
5 |
|
|
5 |
7 |
|
| 18 |
|
5 |
|
|
5 |
7 |
|
| 19 |
|
5 |
|
|
5 |
7 |
|
| 20 |
|
5 |
|
|
5 |
7 |
|
| 21 |
|
5 |
|
|
5 |
7 |
|
| 22 |
|
5 |
|
|
5 |
7 |
|
| 23 |
|
5 |
|
|
5 |
7 |
|
| 24 |
|
5 |
|
|
5 |
7 |
|
| 25 |
|
5 |
|
|
5 |
7 |
|
Nonequivalent Group Design
Table 3-1
(cont.)
| 1 | 2
| 3 | 4
| 5 | 6
| 7 | 8
|
| Person | Pretest
X
from
Table 1-1
| Pretest
Group
Difference
| Pretest
(X) for
Nonequi-
valent
Groups
| Posttest
Y
from
Table 1-1
| Posttest
Group
Difference
| Effect of
Program
(G)
| Posttest
(Y) for
Nonequi-valent
Groups
|
| 26 |
|
0 |
|
|
0 |
0 |
|
| 27 |
|
0 |
|
|
0 |
0 |
|
| 28 |
|
0 |
|
|
0 |
0 |
|
| 29 |
|
0 |
|
|
0 |
0 |
|
| 30 |
|
0 |
|
|
0 |
0 |
|
| 31 |
|
0 |
|
|
0 |
0 |
|
| 32 |
|
0 |
|
|
0 |
0 |
|
| 33 |
|
0 |
|
|
0 |
0 |
|
| 34 |
|
0 |
|
|
0 |
0 |
|
| 35 |
|
0 |
|
|
0 |
0 |
|
| 36 |
|
0 |
|
|
0 |
0 |
|
| 37 |
|
0 |
|
|
0 |
0 |
|
| 38 |
|
0 |
|
|
0 |
0 |
|
| 39 |
|
0 |
|
|
0 |
0 |
|
| 40 |
|
0 |
|
|
0 |
0 |
|
| 41 |
|
0 |
|
|
0 |
0 |
|
| 42 |
|
0 |
|
|
0 |
0 |
|
| 43 |
|
0 |
|
|
0 |
0 |
|
| 44 |
|
0 |
|
|
0 |
0 |
|
| 45 |
|
0 |
|
|
0 |
0 |
|
| 46 |
|
0 |
|
|
0 |
0 |
|
| 47 |
|
0 |
|
|
0 |
0 |
|
| 48 |
|
0 |
|
|
0 |
0 |
|
| 49 |
|
0 |
|
|
0 |
0 |
|
| 50 |
|
0 |
|
|
0 |
0 |
|
Nonequivalent Group Design
Figure 3-1
Nonequivalent Group Design
Figure 3-2
Nonequivalent Group Design
Figure 3
 Simulation Home Page
Simulation Home Page
Copyright © 1996, William M.K. Trochim




