where each O indicates an observation or measure on a group of
people, the X indicates the implementation of some treatment or
program, separate lines are used to depict the two groups in the
study, the R indicates that persons were randomly assigned to
either the treatment or control group, and the passage of time
is indicated by moving from left to right. We will assume that
we are comparing a program and comparison group (instead of two
programs or different levels of the same program).
You will use the data you created in the first exercise. Copy
the pretest scores from the first exercise (Table 1-1, column
5) into column 2 of Table 2-1. Now we need to randomly assign
the 50 persons into two groups. To do this, roll one die for
each person. If you get a 1,2, or 3, consider that person to
be in the program group and place a ‘1’ in the column
3 of Table 2-1 labeled “Group Assignment (Z)”.
If you get a 4, 5, or 6, consider that person to be in the comparison
group and place a ‘0’ in the column 3. Now, imagine
that you give the program or treatment to the people who have
a '1' for Group Assignment and that the program has a positive
effect. In this simulation, we will assume that the program has
an effect of 7 points for each person who receives it. This "Hypothetical
Program Effect" is shown in column 4 of Table 2-1. To determine
the treatment effect for each person, multiply column 3 by column
4 and place the result in column 5 labeled “Effect of Program
(G)”. (The G stands for how much each person Gains as
a result of the program.) You should have a value of ‘7’
for all persons randomly assigned to the program group and a value
of ‘0’ for those in the comparison group. Why
did we multiply the column of 0 and 1 values by the column of
7s when we could just as easily have told you to simply put a
7 next to each program recipient? We do it this way because it
illustrates how a 0,1 variable, called a "dummy variable,"
can be used in a simple formula to show how the Effect of the
Program is created. In this simulation, for instance, we can
summarize how the program effect is created using the formula
where G is the gain or program effect, Z is the dummy coded (0,1)
variable in column 3 and the 7 represents the constant shown in
column 5.
Next, copy the posttest values (Y) from the first exercise (Table
1-1, column 6) to column 6 of Table 2-1 labeled “Posttest
(Y) from Table 1-1". Finally, to create the observed posttest
value that has a program effect built in, add the values in column
5 and 6 in Table 2-1 and put them into column 7 labeled "Posttest
(Y) for Randomized Experimental Design”. You should recognize
that this last column in Table 2-1 has the same posttest scores
as in the first simulation exercise, except that each randomly
assigned program person has 7 extra points that represent the
effect or gain of the program.
As before, you should graph the univariate distributions for the
pretest and posttest in Figures 2-1 and 2-2. But here, unlike
in the first exercise, the 50 people are randomly divided into
two groups. It would be nice if you could distinguish the scores
of these two groups in your graphs of the distributions. You
should do this by using different colored pens or pencils and
lines that slant in different directions for the program and comparison
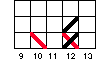
cases. For instance, let's say that the first four persons in
Table 2-1 have the following pretest scores and group assignments
in Table 2-1:
In this case, the histogram for these four persons would look
like

Now plot the data for all 50 persons for both the pretest (Figure
2-1) and posttest (Figure 2-2) making sure to distinguish between
the two randomly assigned groups both color and in the angle of
the mark you make. As in the first simulation, you should estimate
the central tendency for both the pretest and posttest, but here
you should do it separately for the program and comparison cases.
Now, plot the bivariate distribution in Figure 2-3. Again, you need to have a system for distinguishing between program and comparison cases when they fall in the same box. Use different colored pens or pencils for each. In addition, use different marks according to the following system:
First program case  , first comparison case
, first comparison case  ,
second program case
,
second program case  , second comparison case
, second comparison case  .
.
So, if you have a pre-post pair that happens to have two program
and two comparison cases, the graph should look like  .
.
Now, plot the lines on the bivariate plot that describe the pre/post
relationship (as described in the first simulation exercise),
doing a separate line for the program and comparison groups.
There are several things you should note. First, the pretest
central values for the two groups should be similar (although
they are not likely to be exactly the same). This is, of course,
because the groups were randomly assigned. Second, the posttest
central values should clearly differ. In fact, we expect that
the difference between the average posttest values should be approximately
the 7 units that you put in. In addition, the vertical difference
between the relationship lines in the bivariate plot (Figure 2-3)
should also be about 7 units.
At this point you should be convinced of the following:
• The design simulated here is a very simple single-factor
randomized experiment. The single factor is represented by the
0,1 treatment variable that represents which group people are
in. You could simulate more complex designs. For example, to
simulate a randomized block design you would first rank all persons
on the pretest. Then you could set the block size, for example
at n = 2. Then, beginning with the lowest two pretest scorers,
you would randomly assign one to the program group and the other
to the comparison group. You could do this by rolling a die--if
you get a 1, 2, or 3 the lowest scorer is a program participant;
if you get a 4, 5, or 6 the higher scorer is. Continuing in this
manner for all twenty-five pairs would result in a block design.
• You could also simulate a 2 x 2 factorial design. Let's say that you wanted to evaluate an educational program that was implemented in several different ways. You decide to manipulate the manner in which you teach the material (Lecture versus Printed Material) and where the program is given (In-class or Pull-out). Here you have two factors -- Delivery of Material and Location -- and each factor has two levels. We could summarize this design with a simple table that shows the four different program variations you are evaluating

• You should recognize that the design simulated here can
be considered a repeated measures experimental design because
a pretest and posttest are used. You could simulate a posttest-only
experimental design as well.